Living in a World of Catenaries..
Looking up at a web of hanging cables, in the city, can surely give an impression that it is messy and chaotic. A picture above depicts my impression of a person, startled in the middle of a street, with a thought about the hanging cables- “All the cables are sagging downwards to Earth. Could there be a common ‘pattern’ in shapes of all these hanging cables?”
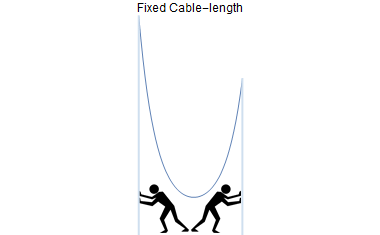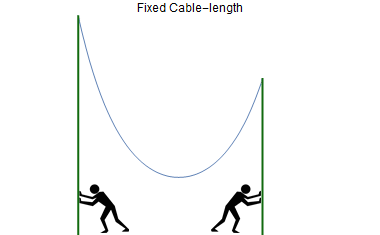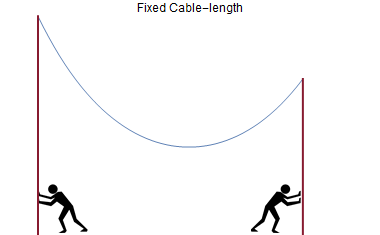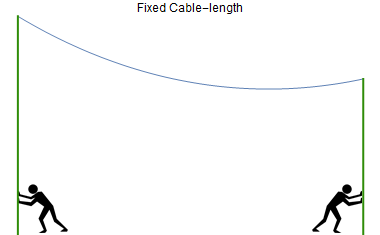
The person sets his first experiment- He takes a cable of a fixed length and ties it to the top of two poles of different heights. Further, he moves the poles back and forth and notes down the shape of the cable in response to the change of distance between the two poles. (See an animation.)
However, to understand the underlying pattern if any, he would need Mathematics and Physics.
Historic Perspective
Catenary
In 17th century, Galileo got interested in this problem of hanging chords, and thought that the shape of all the hanging chords is approximately a parabola. He was close! But, it took advent of Calculus to crack this problem. Later in 1691, G. Leibniz, C. Huygens, and J. Bernoulli figured out an equation for the shape of the hanging cable. The shape is not a parabola but, a curve later became famously known as Catenary.
Inverted Catenary Arch
Arches are typically used to support weights of the bulding structures. Robert Hooke solved the problem of optimal shape of the arch and published the solution in 1675. To build an arch, a chain can be hung, and the shape of it (catenary) can be transferred to a form. Later, the form can be used as a guidline for constrcting the archs.
Below is a catenary arch supporting a roof of Keleti railway station at Budapest, Hungary.
Equating the Rate of change of Something
Static Equilibrium
A steady hanging cable can be considered at static equilibrium. That means if we choose a segment of a cable (A to B), then all the forces, acting on it, must cancel out.
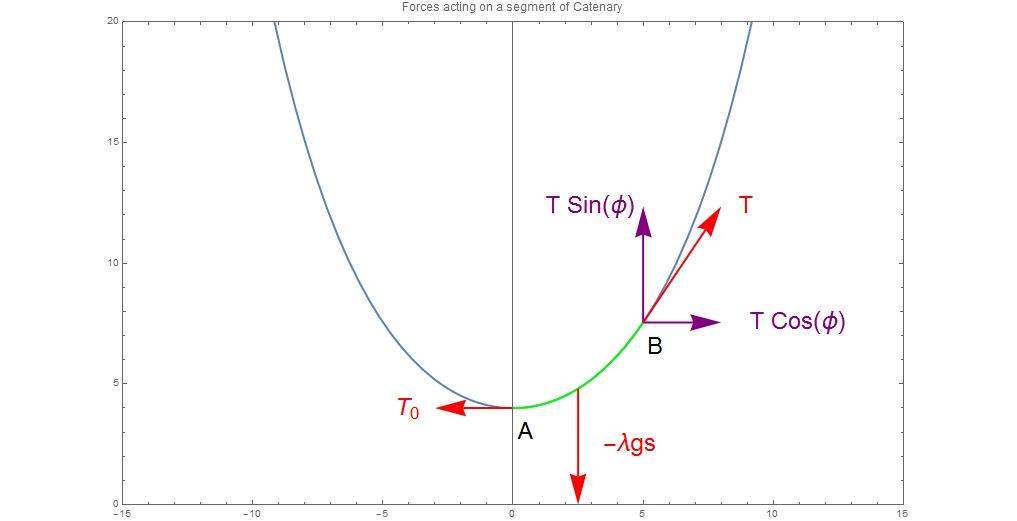

Second-order Differential Equation
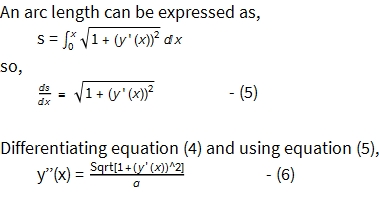
A General Solution
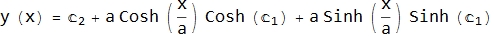
Unknown constants in the general solution can be determind with initial conditions.
Arc-length vs. Area under the Arc
One geometric aspect of the catenary is worth mentioning. If you pick a horizontal interval (x1 to x2) of a catenary, then a ratio of an area under that interval to the arc-length over that interval remains constant, irrespective of the choice (for example, a size) of the interval.
A following interactive example demonstrates the special property of the catenary. It is said that in plane curves, apart from a horizontal line, only catenary possesses this property.
Interact with the Catenaries
Here, the catenary is supported with two poles of different height. You can manipulate two locators situated at the top of the poles to adjust heights and the separation between the poles. Be patient! As with this manipulation, you have changed the ‘initial conditions’ and the differential equation will be solved on the cloud to plot the new catenary. You may control the value of ‘a’ and observe its effect on the shape of the catenary.
Catenoid
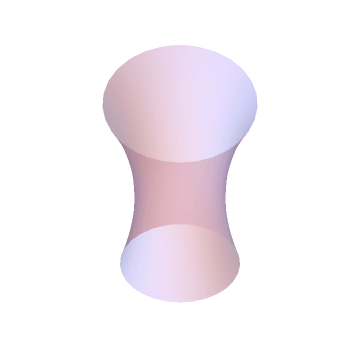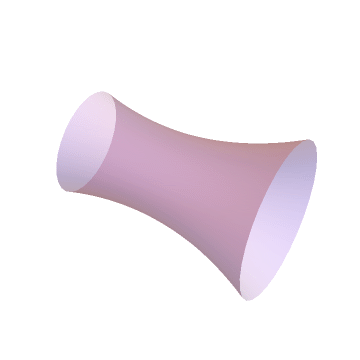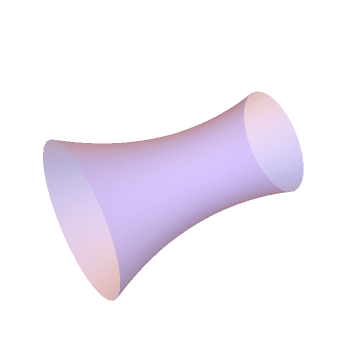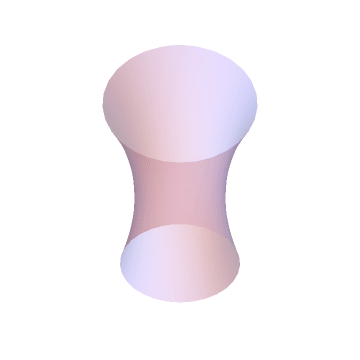
Let’s go in three dimensions! If we revolve a catenary along the X-axis, you form a 3D surface, called Catenoid. A soap bubble, supported between two rings of different radii, attaines the same shape. The soap film tends to minimize the surface-tension energy and consequently, it takes the shape of catenoid.
Change in a World-view
To me, catenary has changed the way I see various slacking things around me. Not just that.. it reminds me the power of mathematics and physics that the problem solvers achieved in 17th century.
- https://en.wikipedia.org/wiki/Catenary
- https://vanderbei.princeton.edu/WebGL/catenoid_explanation.html
- https://mathematica.stackexchange.com/a/9687